R-Line
Introduction
R-Line is a random line segment generator. It produces random values at regular rate, and then linearly interpolates between them. The algorithm has audio-rate parametric control of both the range and rate of change for generated values.
This algorithm is a great little control signal generator that can add a bit of zest to an otherwise static parameter in a patch. It's a very efficient way to add a warm organic feel to a patch.
Notable Implementation Details
This particular algorithm uses a fixed-point phasor similar to the ones seen in osc and fmpair. Fixed point has very good numerical stability, which makes it ideal for a phasor algorithm.
To keep things more portable, R-Line implements its own
pseudo-Random Number Generator (pRNG), using a common
algorithm generating random values known as
Linear Congruential Generator, or an LCG. This is
what most rand function
implementations use under the hood. The modulus, multiplier,
and and increment values come from the Microsoft
Visual/Quick C/C++ library (as found on Wikipedia).
Tangled Files
R-Line tangles to a C file and a header file.
The C file rline.c contains the core implementation
code.
#include <math.h>
#define SK_RLINE_PRIV
#include "rline.h"
<<macros>>
<<funcs>>The header file rline.h contains forward function
declarations. When SK_RLINE_PRIV is enabled, the structs
are exposed. Otherwise, they are left as opaque.
#ifndef SK_RLINE_H
#define SK_RLINE_H
#ifndef SKFLT
#define SKFLT float
#endif
<<typedefs>>
<<funcdefs>>
#ifdef SK_RLINE_PRIV
<<structs>>
#endif
#endifCore Struct
The core struct is called sk_rline.
typedef struct sk_rline sk_rline;NOTE: the jitseg_struct block is explicitly
delcared after the sk_rline struct because of
dependencies. See: jitseg.
struct sk_rline {
<<sk_rline>>
};
<<jitseg_struct>>Constants and Variables
The value from the LCG is often scaled to be normalized
between 0 and 1. The constant required for this
is 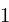 ,
or
,
or 1/((1L<<31) - 1). This value is
stored in a constant.
SKFLT rngscale;rl->rngscale = 1.0 / ((1L<<31) - 1);The current state of the random number generator is stored
as an integer rng. It is initialized to be seed.
int rng;rl->rng = seed;
<<set_random_scaler>>
<<generate_initial_values>>The fixed point phasor has two major constants: the maximum length, as well as the masking value. Detailed explanation of these are beyond the scope of this document. For more information, consult the relevant sections in osc.
#define SK_RLINE_PHSLEN 0x1000000L
#define SK_RLINE_PHSMSK 0xFFFFFFLThe variable maxlens is maximum phasor length converted to
units of seconds by dviding it by the sampling rate.
Multipyling this value with a frequency will return an
increment value in units of phasor, which is used
as the phasor increment value.
SKFLT maxlens;rl->maxlens = (SKFLT)SK_RLINE_PHSLEN / sr;Phase position is stored in an unsigned long called
phspos. When it needs to be converted for use in floating
point operations , the constant scale is used.
unsigned long phasepos;
SKFLT scale;rl->phasepos = 0;The scale value works by normalizing to be in the range 0-1
by dividing by the max phase length SK_RLINE_PHSLEN, then
scaling it to be the difference between the start/end point
values. Doing this shaves off a divide operation later.
rl->scale = (rl->end - rl->start) / SK_RLINE_PHSLEN;A line has two points: a start point, and an end point.
These are stored as normalized floating point variables
start and end, and then are dynamically scaled to the
min and max values during computation.
SKFLT start;
SKFLT end;rl->rng = LCG(rl->rng);
rl->start = RNG(rl->rng) * rl->rngscale;
rl->rng = LCG(rl->rng);
rl->end = RNG(rl->rng) * rl->rngscale;
<<calculate_initial_scale>>Linear Congruential Generator
An internal Linear Congruential Generator is used to generate sequences of pseudo-random numbers.
It is the following equation
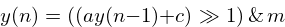
Where 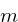 is the masking value
is the masking value
0x7ffffff, 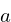 is a
is a
multiplier, and 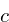 is the
is the
increment. In this
implementation, 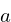 will be
will be 0x343fd,
and 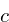 will be
will be
0x2693ec3. These constants come from the wikipedia page
on LCGs.
The LCG here can be implemented as a stateless function or macro. In this case, we will go with the macro.
#define LCG(y) (y * 0x343fd + 0x269ec3)The LCG operation only computes the next state state of
the random-number generator. To actually get it within the
correct bounds for this sytem, it has to be right-shifted
to knock it down 1 bit, then masked by 0x7ffffff as a kind
of modulo operation.
This macro operation RNG assumes that y is the current
state of the LCG.
#define RNG(y) ((y >> 1) & 0x7fffffff)Initialization
Initialization is done with sk_rline_init.
The main things needed for initialization are the sampling
rate sr, as well as the initial seed value for the random
number generator.
void sk_rline_init(sk_rline *rl, int sr, int seed);void sk_rline_init(sk_rline *rl, int sr, int seed)
{
<<init>>
}Parameters
Minimum value
Set with sk_rline_min.
void sk_rline_min(sk_rline *rl, SKFLT min);void sk_rline_min(sk_rline *rl, SKFLT min)
{
rl->min = min;
}SKFLT min;Initialized to be 0.
sk_rline_min(rl, 0);Maximum value
Set with sk_rline_max.
void sk_rline_max(sk_rline *rl, SKFLT max);void sk_rline_max(sk_rline *rl, SKFLT max)
{
rl->max= max;
}SKFLT max;Initialized to be 1.
sk_rline_max(rl, 1);Rate
Set with sk_rline_rate.
void sk_rline_rate(sk_rline *rl, SKFLT rate);void sk_rline_rate(sk_rline *rl, SKFLT rate)
{
rl->rate= rate;
}SKFLT rate;Initialized to be an arbitrary default value 1.
sk_rline_rate(rl, 1);Computing a sample
A single sample is computed with sk_rline_tick.
SKFLT sk_rline_tick(sk_rline *rl);SKFLT sk_rline_tick(sk_rline *rl)
{
SKFLT out;
out = 0;
<<compute_current_sample>>
<<update_phase>>
<<generate_next_line_segment>>
return out;
}Compute the current sample. The line interpolation is calculated in a normalized space, then scaled to be in the min/max range. Doing it this way allows the min/max values to be dynamically changed over time without having to wait for the next line.
The normalized output can be computed with the expression:
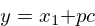
Where 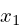 is the starting point
of the line,
is the starting point
of the line, 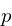 is
the current phase increment, represented in fixed point, and
is
the current phase increment, represented in fixed point, and
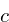 is the constant that normalizes
and scales the phase to be the amount of progress to value
is the constant that normalizes
and scales the phase to be the amount of progress to value
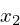
out = rl->start + rl->phasepos*rl->scale;
out = out * (rl->max - rl->min) + rl->min;Update phase position. The phase is updated by incrementing it by a amount obtained by multiplying the frequency by the maximum phase length in units of seconds. How this works is beyond the scope of this document, but is explained in osc.
rl->phasepos += floor(rl->rate * rl->maxlens);Generate next line segment. Preparation for a new line segment happens when the phase of the phasor reaches the end, and is greater than or equal to the max length. The phasor is masked in order to filter out upper bits and allow the lower bits to roll over. The the starting value is set to be the current end value, and a new end value is obtained using the random number generator.
After the new points have been obtained, the constant used to normalize + scale the phasor value is computed. Dividing by the maximum phasor length normalizes the phasor to be in range 0 and 1. Multiplying by the difference of the two segment values scales this value to be in the correct range. This constant is useful because it shaves off a divide operation, which has traditionally been a costly arithmetic computatoin compared to a multiply.
if (rl->phasepos >= SK_RLINE_PHSLEN) {
rl->phasepos &= SK_RLINE_PHSMSK;
rl->start = rl->end;
rl->rng = LCG(rl->rng);
rl->end = RNG(rl->rng) * rl->rngscale;
rl->scale = (rl->end - rl->start) / SK_RLINE_PHSLEN;
}Variation: Jitseg
jitseg is a variation of rline that uses another
instances of rline to modulate the frequency. Typically,
a signal generator like this is added to anotherwise
steady signal to add small deviations and detail to the
sound. This kind of low-level low-frequency is often known
as jitter.
It is equivalent to the following LIL pseudo-code
rline vmin vmax [rline rmin rmax rrate]Where vmin and vmax are the min/max values,
rmin and rmax values determine the range of
rate, and rrate determines the rate of change
controling the main rline rate.
typedef and struct (sk_jitseg)
typedef struct sk_jitseg sk_jitseg;struct sk_jitseg {
sk_rline main;
sk_rline rate;
};Initialization
sk_jitseg_init initializes both rlines with separate
seeds. s1 is main. s2 is rate.
void sk_jitseg_init(sk_jitseg *js, int sr, int s1, int s2);void sk_jitseg_init(sk_jitseg *js, int sr, int s1, int s2)
{
sk_rline_init(&js->main, sr, s1);
sk_rline_init(&js->rate, sr, s2);
}Parameters
Two rlines combined yields two separate min/max pairs. One pair for the output value range, and one pair for the range of rate of which these values change. The rate at which value rate changes can be set as well.
void sk_jitseg_min(sk_jitseg *js, SKFLT min);
void sk_jitseg_max(sk_jitseg *js, SKFLT max);
void sk_jitseg_rate_min(sk_jitseg *js, SKFLT min);
void sk_jitseg_rate_max(sk_jitseg *js, SKFLT min);
void sk_jitseg_rate_rate(sk_jitseg *js, SKFLT rate);
SKFLT sk_jitseg_tick(sk_jitseg *js);Min/Max Values
void sk_jitseg_min(sk_jitseg *js, SKFLT min)
{
sk_rline_min(&js->main, min);
}
void sk_jitseg_max(sk_jitseg *js, SKFLT max)
{
sk_rline_max(&js->main, max);
}Min/Max Rates
void sk_jitseg_rate_min(sk_jitseg *js, SKFLT min)
{
sk_rline_min(&js->rate, min);
}
void sk_jitseg_rate_max(sk_jitseg *js, SKFLT max)
{
sk_rline_max(&js->rate, max);
}Rate of Rate Modulator
void sk_jitseg_rate_rate(sk_jitseg *js, SKFLT rate)
{
sk_rline_rate(&js->rate, rate);
}SKFLT sk_jitseg_tick(sk_jitseg *js)
{
SKFLT out;
out = 0;
sk_rline_rate(&js->main, sk_rline_tick(&js->rate));
out = sk_rline_tick(&js->main);
return out;
}