dblin

Overview

dblin is a computationally efficient decibel-to-linear converter. Given a input value, such as -3dB, it will return an output value of ~0.707945, which could then be used to attenuate another signal.

There are three things done to make this efficient:

The usual conversion formula is reworked to use a base-e exponential (exp) instead of a base-10 power (pow). Traditionally, exp is a much cheaper function pow (however, modern optimizing compilers will make this negligble).

The conversion removes any use of division and works those components into constants.

parameter caching is used, which prevents computation from happening if it doesn't need to be done.

From "pow" to "exp"

One of the cleverer parts of this implementation is to rework the conventional formula for dB to linear conversion to use the base-e exponent via the exp function instead of base-10 via pow. Traditionally, this has had performance gains. Admittedly, modern C compilers seem to optimize this if you use something like -O3. But, the approach is still pretty neat.

The conventional way to convert a dB unit to a linear one is like this:

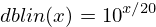
$dblin(x) = 10^{x/20}$

This eventually gets derived to this:

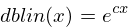
$dblin(x) = e^{cx}$

Where 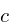is the constant 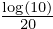$\log(10) \over 20$ . This will be returned to in a moment.

Converting between dB and linear space can be presented in the following way:

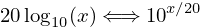
$20\log_{10}(x) \Longleftrightarrow 10^{x/20}$

The log10 function can be recreated using natural logs with this identity:

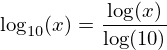
$\log_{10}(x) = {\log(x) \over \log(10)}$

It is also helpful to remember this relationship between natural logs and e exponents:

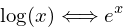
$\log(x) \Longleftrightarrow e^{x}$

In a bit of a hand-wavey way, this identity can be established.

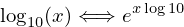
$\log_{10}(x) \Longleftrightarrow e^{x\log{10}}$

Which, subsituting the log10 expression from above, looks like this:

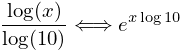
${\log(x) \over \log(10)} \Longleftrightarrow e^{x\log{10}}$

Adding in the 20

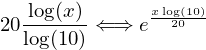
$20 {\log(x) \over \log(10)} \Longleftrightarrow e^{{x\log(10)} \over {20}}$

log10 can be brought back in for clarity.

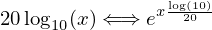
$20\log_{10}(x) \Longleftrightarrow e^{x{{\log(10)} \over {20}}}$

This relationship won't be formally proven, but one can sort of see the balance. Where there's a log, there's an e exponent on the other side. Where there's a multiply, there's a divide, etc.

Finally, the constant parts of the expression separated, which gives the correspondance using the final formula:

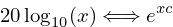
$20\log_{10}(x) \Longleftrightarrow e^{xc}$

And that's what this algorithm implements in code. That's it.

Tangled Files

dblin.c and dblin.h.

<<dblin.h>>=

#ifndef SK_DBLIN_H
#define SK_DBLIN_H

#ifndef SKFLT
#define SKFLT float
#endif

#ifdef SK_DBLIN_PRIV
<<structs>>
#endif

<<typedefs>>
<<funcdefs>>
#endif

<<dblin.c>>=

#include <math.h>

#define SK_DBLIN_PRIV
#include "dblin.h"

<<funcs>>

Struct Initialization

sk_dblin.

<<typedefs>>=

typedef struct sk_dblin sk_dblin;

Three values stored. The constant c, the previous input value prev, and a cached output value out.

<<structs>>=

struct sk_dblin {
    SKFLT c;
    SKFLT prev;
    SKFLT out;
};

<<funcdefs>>=

void sk_dblin_init(sk_dblin *dl);

<<funcs>>=

void sk_dblin_init(sk_dblin *dl)
{
    dl->c = log(10) / 20.0;
    dl->prev = 0;
    dl->out = 1;
}

Computation

A single sample of an audio-rate signal is computed with with sk_dblin_tick, which expects an input signal db.

<<funcdefs>>=

SKFLT sk_dblin_tick(sk_dblin *dl, SKFLT db);

In this function, the current input value is checked against the previous to see if there has been any change. If there has, the cached output value is updated.

<<funcs>>=

SKFLT sk_dblin_tick(sk_dblin *dl, SKFLT db)
{
    SKFLT out;

    out = dl->out;

    if (db != dl->prev) {
        out = exp(db * dl->c);
        dl->out = out;
        dl->prev = db;
    }

    return out;
}