Bezier
Overview
bezier implements a quadratic
bezier curve mapper.
An input value between 0 and 1 goes in,
and a bezier curve output comes out. The control
point is controlled via X and Y parameters, presumably in
the normalized range 0-1.
Tangled Files
#include <math.h>
#include "bezier.h"
<<static_funcdefs>>
<<funcs>>#ifndef SK_BEZIER_H
#define SK_BEZIER_H
#ifndef SKFLT
#define SKFLT float
#endif
<<funcdefs>>
#endifA bit of math
The equation for a quadratic Bezier curve is the following:
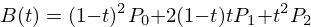
Where 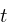 is a normalized time
value between 0 and 1,
and
is a normalized time
value between 0 and 1,
and 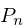 refers to a
2-dimensional point with a (x,y) coordinate.
refers to a
2-dimensional point with a (x,y) coordinate.
The issue with the classic equation above is that the value
is derived from 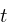 , allowing
, allowing
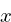 to be fractional. This is
problematic because the system implemented here is
discrete, restricted to whole-integer values of
to be fractional. This is
problematic because the system implemented here is
discrete, restricted to whole-integer values of 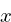 .
.
The solution to this problem is to rework the equation
above to solve for $t$ in terms of the current sample
position 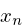 . Once $t$ is found, it can be used to
compute the result, which is the y component of the bezier
curve in terms of t.
. Once $t$ is found, it can be used to
compute the result, which is the y component of the bezier
curve in terms of t.
The Bezier x component 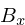 can
be rearranged to be a quadratic equation for
can
be rearranged to be a quadratic equation for 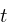 , given the x bezier control points
, given the x bezier control points
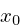 ,
,
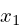 , and
, and
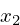 , as well as the current
sample position
, as well as the current
sample position 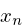 .
.
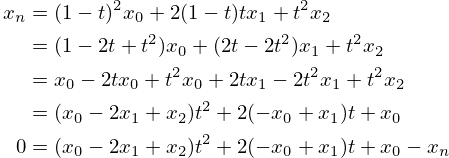
This yields the following
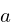 ,
,
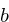 , and
, and
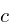 quadratic equation
coefficients:
quadratic equation
coefficients:
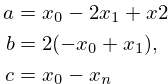
Using those variables and the quadratic equation, the value
of 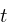 can be found if it is a real
value.
can be found if it is a real
value.
This value is implemented in a C function called find_t,
along with a quadratic equation quadratic_equation.
static SKFLT find_t(SKFLT x0, SKFLT x1, SKFLT x2, SKFLT x);static SKFLT find_t(SKFLT x0, SKFLT x1, SKFLT x2, SKFLT x)
{
SKFLT a, b, c;
a = (x0 - 2.0 * x1 + x2);
b = 2.0 * (-x0 + x1);
c = x0 - x;
if (a) {
return quadratic_equation(a, b, c);
} else {
return (x - x0) / b;
}
}static SKFLT quadratic_equation(SKFLT a, SKFLT b, SKFLT c);static SKFLT quadratic_equation(SKFLT a, SKFLT b, SKFLT c)
{
SKFLT det; /* determinant */
det = b*b - 4*a*c;
if (det >= 0) {
return ((-b + sqrt(det))/(2.0*a));
} else {
return 0;
}
}Bezier Compute
Now, with all the mathematical derivations out of the way,
a bezier curve can be computed given an x position xpos,
and a control point at cx and cy.
SKFLT sk_bezier_tick(SKFLT xpos, SKFLT cx, SKFLT cy);In total the bezier takes in 3 points, with the middle point being the control point, and the end points being with the normalized ranges (0, 0) and (1, 1).
SKFLT sk_bezier_tick(SKFLT xpos, SKFLT cx, SKFLT cy)
{
SKFLT x[3];
SKFLT y[3];
SKFLT t;
SKFLT val;
x[0] = 0;
x[1] = cx;
x[2] = 1;
y[0] = 0;
y[1] = cy;
y[2] = 1;
t = find_t(x[0], x[1], x[2], xpos);
val = (1.0-t)*(1.0-t)*y[0] + 2.0*(1 - t)*t*y[1] + t*t*y[2];
return val;
}