Linear Congruent Generator

Overview

A Linear Congruent Generator, or LCG, is a very common algorithm used to produce a sequence of pseudorandom numbers.

An LCG is contained in many of the algorithms here, including rline (rline), bigverb (bigverb), sparse (sparse), and trand (trand). The core API also has a global RNG that is an LCG.

Wikipedia is a great resource on the subject: https://en.wikipedia.org/wiki/Linear_congruential_generator.

LCG parameters used in the sndkit LCGs come from this page.

Definition

A generalized LCG can be defined using the following expression:

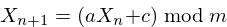
$X_{n + 1} = (aX_n + c) \bmod m$

Where 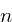is the sample number, 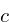is the increment, 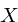is the state, 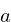is the multiplier, and 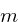is the modulus.

Typical Implementation in sndkit

Because sndkit favors self-contained algorithms, a similar LCG has been reimplemented many times. Fortunately, the algorithm itself is quite simple, and only requires a few lines of code with some magic numbers.

The typical implementation is a 32-bit LCG with a multiplier a of 1103515245, increment c of 12345, and a modulus m of 2^31.

An LCG requires a 32-bit integer to store state. It can also be helpful to have a constant of 2^31, which is 2147483648.

The C code can be reduced down to this expression;

unsigned long rng;
rng = seed;
rng = (1103515245 * rng + 12345) % 2147483648;

Where seed is some initial seed, and rng is the state;